<A>
function-theory: *
an example of real analysis is the Fibonacci numbers, the integer sequence whose elements are the sum of the previous two elements. The first two elements are either 0 and 1 or 1 and 1 so that the sequence is (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...). This sequence is found in many natural occurrences.
IMAGE BELOW
A tiling with squares whose side lengths are successive Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13 and 21

<B>
algebra of logic: *
IMAGE BELOW a logic circuit
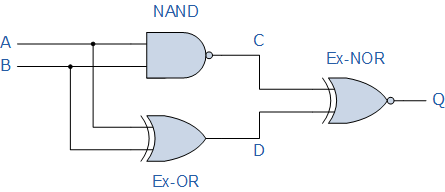
Below is the Boolean Algebra Truth Table for the logical functions above, points C, D and Q. The circuit consists of a 2-input NAND gate, a 2-input EX-OR gate & finally a 2-input EX-NOR gate at the output. With 2 inputs to the circuit labelled A and B, there can only be 4 possible combinations of the input:: 0-0, 0-1, 1-0 & 1-1. Plotting the logical functions from each gate in provides the following truth table- :
