<A>
Kant (and mathematics): *
Kant was a student & a teacher of mathematics throughout his career & his reflections on mathematics had a profound impact on his thinking. He developed philosophical views on the status & nature of mathematics, axioms & proof & the relation between pure mathematics & nature. Maths was even instrumental in his approach to the general question “how are synthetic judgments a priori possible?” which was shaped by his view of mathematics.
In the Prize Essay (1764), he compared mathematics & metaphysics. He defined the mathematical concept of a trapezium as the arbitrary combination of other concepts (“four straight lines bounding a plane surface so that the opposite sides are not parallel to each other”) & concluded that mathematics could not be used to find philosophical or metaphysical truths, because “geometers acquire their concepts by means of synthesis, whereas philosophers…by means of analysis”. In his essays “Concerning the Ultimate Ground of the Differentiation of Directions in Space” and “On the Form and Principles of the Sensible and the Intelligible World” (both 1768) he worked to establish the orientability & actuality of a Newtonian-style absolute space, which was the object of geometry as he understood it. In his Critique of Pure Reason (1781) he claimed that mathematical cognition derives from the construction of its concepts that exhibit a priori the intuition corresponding to it. He uses the example of a triangle, defined as a rectilinear figure contained by 3 straight lines (Euclid), but notes the concept is constructed only when such a definition is paired with a corresponding intuition. When one so renders a triangle to perform the steps necessary for geometric proof, one does so a priori; the object displayed does not borrow its pattern from any experience. Universal truths about all triangles can be derived from a single triangle, as all triangles exhibit the general concept triangle, which also corresponds to a priori intuition. Kant claims that “properly mathematical judgments are always a priori judgments”; they are necessary & cannot be derived from experience. He illustrates with the proposition “7 + 5 = 12”. Only intuition, not experience nor logical analysis provides the answer, 12. He follows this discussion of arithmetic reasoning with corresponding claims about Euclidean geometry, according to which the principles of geometry express synthetic relations between concepts. He posits all mathematical judgments, including geometric theorems, as synthetic, not analytic.
<B>
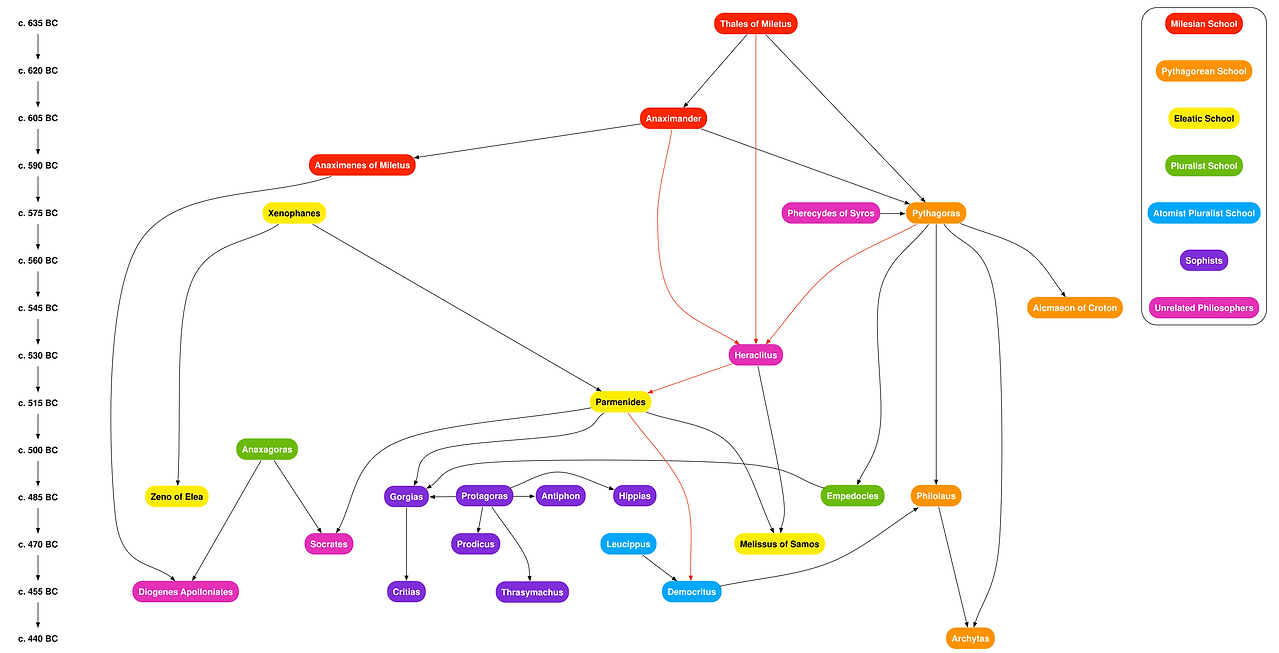
pre-Socratics & Plato: *
aka natural philosophers who investigated the workings of the natural world, human society, ethics & religion, seeking explanations based on natural principles not supernatural. The first pre-Socratic was Thales (624-545 BC), a mathematician, astronomer & philosopher, from Miletus in Ionia, Asia Minor. Diogenes Laërtius divides them into 2 groups: the Ionians, led by Anaximander, and the Italiote, led by Pythagoras. Athens in the 5th century saw a new wave of thinking led by Socrates (470-399 BC). It is through the writings of Plato (428-347 BC) that the teaching of Socrates survived. He was an Athenian philosopher, student of Socrates, founder of the Platonist school of thought & it’s Academy. He invented the written dialogue and dialectic forms in philosophy (derived from Socrates). His contributions include political philosophy (the Republic) & the theory of Forms known by pure reason, in which Plato presents a solution to the problem of universals known as Platonism.
see Illustration
<C>
Plato (and mathematics): *
Plato the mathematician is best known for his identification of 5 regular symmetrical 3D shapes (which he maintained were the basis for the whole universe) known as the Platonic Solids: the tetrahedron the octahedron the icosahedron the cube & the dodecahedron. They were prominent in Plato’s philosophy, he wrote of them in the dialogue Timaeus.
Plato was also a great patron of mathematics. In his The Republic (375 BC), written 75 years before Euclid, he sets out his ideas on education; he made it clear only after mastering mathematics, does one proceed to philosophy. Over the main entrance of his Academy was the phrase "Let None But Geometers Enter Here" Mathematics was taught as a branch of philosophy (following Pythagoras) & the first 10 of a 15 year course involved the study of science & mathematics (arithmetic, plane & solid geometry, astronomy & harmonics). Plato himself taught arithmetic, theory of numbers, advanced geometry & astronomy & demanded accurate definitions, clear assumptions & logical deductive proof; he insisted such proofs be demonstrated with only a straight edge & compass. He posed many mathematical problems (“squaring the circle”, “doubling the cube” and “trisecting the angle”); his students, which included Theaetetus, Eudoxus & Archytas, made most of the major mathematical innovations of the 4th century.
<D>
Zeno (unmathematical: *
Zeno was initially attracted to the Cynics; their motto was 'Ethics alone', which explains his focus on Ethics. It was the ”end” of philosophy, the aim; an adequate account of phenomena (Nature, Physics) & the modes of expression (Rhetoric, Logic) were but the “means”. Zeno established the Stoics; for them ethics not geometry was at the heart of philosophy. Zeno’s primary concern was to establish principles to govern conduct, not merely to state them but to also show they were right. Logic was useful only to detect error, NOT to establish truth; he was an empiricist, he believed what his eyes told him (rather than extended logic). To him (as to Chrysippus) geometry was far less important than to Plato and Aristotle. The Stoics had a strong intuitionist bend & proposed that geometry was a disposition concerned with the products of our minds, which clearly breaks from the Platonic form approach. Instead of focusing on geometry they took biological examples as the sine qua non of their ideas; they sought to account for the emergence of form in bodies rather than the compatibility of form in bodies with preconceived ideas; they cloaked their whole world-theory in an explicitly non-transcendental, non-idealistic garb. They were full on materialists & denied the ideal Form concept critical for Plato.
Chrysippus (279-206 BC), 3rd head of the school, expanded the fundamental doctrines of Zeno & fullly established the Stoa; Chrysippus was a prolific writer & we know of Zeno through him; he wrote on Logic but not based on his interest but because Logic was necessary for ethics. He was also interested in geometry; he solved a problem proposed by Democritus: if a cone is divided by a plane parallel to its base, are the surfaces of the segments equal or unequal? If they are equal, the cone becomes a cylinder; if unequal, the surface of the cone must be stepped. Chrysippus stated the surfaces are both equal & unequal, negating the law of excluded middle with respect to the equal & unequal. He also claimed that one was a number, not just a measure; this was explicitly denied by Aristotle & not generally accepted by the Greeks. He also regarded bodies, surfaces, lines, places, the void and time as all being infinitely divisible; this was the dominant physical hypothesis of the Stoics (that nature is composed of infinitely divisible bodies).
<E>
Epicurus (unmathematical): *
The Epicurean School (states Proclus) unlike the Sceptics, who would do away with all knowledge, proposed only to discredit geometry. Some of them such as Polyaenus, Demetrius of Laconia, and Zeno of Sidon were men well versed in mathematics but all criticized Euclidean geometry. Cicero stated that Polyaenus, an eminent first-generation Epicurean came to believe that “all geometry is false” after he had accepted the views of Epicurus. Zeno, an Epicurean & keen mathematician, criticized Euclid, & sought to show that deductions from the fundamental principles of geometry cannot, on their own, be proved. They stood against both the axioms & principles of geometry as well as its logical completeness. Their rejection was based on their empiricism & their founders prejudice against infinite divisibility. They regarded mathematics & geometry as contributing nothing to the perfection of wisdom. Cicero notes this aversion to geometry & the consequent mathematical ignorance of Epicureans .
<F>
Schopenhauer (unmathematical): *
Schopenhauer was a realist regarding mathematics. In metaphysics, realism states that an object exists in reality independently of the person viewing it. Said object is ontologically independent of someone's conceptual scheme or perceptions, linguistic practices or beliefs. Mathematical realism holds that mathematical entities exist independently of the human mind. Humans do not invent mathematics, but discover it & there is really one sort of mathematics that can be discovered.
In The World as Will and Representation, Schopenhauer was critical of contemporaneous attempts to prove Euclid’s parallel postulate axiom. Writing shortly before the discovery of hyperbolic geometry demonstrated the logical independence of the axiom & before the general theory of relativity revealed it does not necessarily express a property of physical space, he criticized mathematicians for trying to use indirect concepts to prove what he held was directly evident from intuitive perception. Throughout his writings he criticized the logical derivation of philosophies and mathematics from mere concepts, instead of from intuitive perceptions.
<G>
Nietzsche (unmathematical): *
He saw mathematics as a moral activity
"Let us introduce the refinement and rigor of mathematics into all sciences as far as this is at all possible, not in the faith that this will lead us to know things but in order to determine our human relation to things. Mathematics is merely the means for general and ultimate knowledge of man."
aphorism 246- the Gay Science
<H>
Schopenhauer (4th book): *
The initial edition of Will and Representation was published in 1819. Later, in 1844, he published a 2nd edition in two volumes; while the first was a reprint of the original, the second was a new work clarifying his thoughts & giving additional reflections. His views had not changed substantially.
[This seems to follow Spengler’s own publicising history, almost exactly one century later; Decline , (subtitled Form and Actuality) was published, 1918; a second volume (subtitled Perspectives of World History), was published in 1922. Perspectives of World History addresses some of his critics but adds little to the original work. The definitive edition of both volumes was published in 1923.]
<I>
Nietzsche: (illogical): *
Nietzsche’s own work is littered with inconsistency & contradiction. He denounces “will” in Beyond Good & Evil but then posts “Will to Power”; in the same work he denies any sort of morality but then advances formulas for greatness & recipes for virtue! In The Will to Power (1901) he denounces “causality” only to then advocate “power” in a clear notion of causation. In The Anti-Christ (1888) he clearly reflects hostility towards Christianity, but then informs us that Jesus was a “free spirit”. As a classical scholar Nietzsche certainly knew Aristotelian logic; in Beyond Good & Evil (1886) he used a reducio ad absurdum argument against an opponent; he had certainly read Kant & Hegel. However there is no indication that he read or was aware of the ground breaking pioneers of 19th century logic. In 1847 De Morgan & G Boole (father of Boolean algebra) published Formal Logic and Mathematic Analysis of Logic. Frege (a German), the father of analytic philosophy, published his seminal Conceptual Writing in 1879 and Foundations of Arithmetic in 1884.