80.
conquering Goths *
The Goths flourished in Europe throughout ancient times and into the middle Ages. The Romans referred to them as “barbarians,”; they are famous for sacking Rome in 410 AD. Ironically, they also helped preserve Roman culture. After the sacking of Rome, a group of Goths moved to Gaul (in modern-day France) and Iberia and formed the Visigoth Kingdom. They would eventually incorporate Catholic Christianity, Roman artistic traditions and other aspects of Roman culture. The last Gothic kingdom fell to the Moors in A.D. 711.
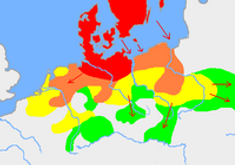
homelands & initial expansion of the Germanic tribes 750 BC – AD 1
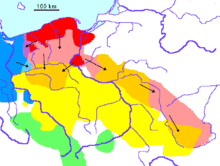
movement into central Europe after AD 1;

onto the Black Sea by 4th century AD.
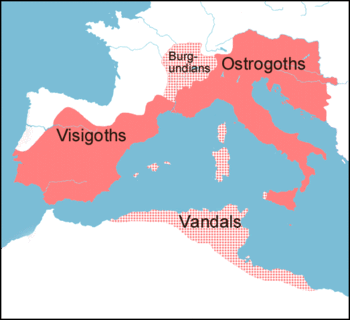
Eventually they toppled Rome & occupied the Western Empire; this map shows the maximum extent of territories ruled by Theodoric the Great in 523 AD
81.
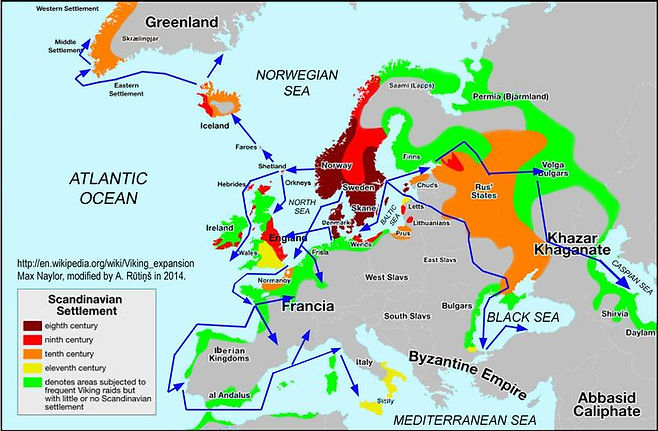
conquering Vikings: *
Facilitated by advanced sailing & navigational skills, using the longship, Vikings sailed into the Mediterranean,, N. Africa, Middle East & Central Asia. Following extended phases of sea & river-borne exploration, expansion and settlement, Viking (Norse) communities and polities were established in diverse areas of north-western Europe, European Russia, the North Atlantic islands and as far as the north-eastern coast of North America.
82.
Gauss (& Euclidean geometry, axiom of parallels): *
In 1800 there was only 1 geometry (what we call Euclidian geometry); for 2,000 years Euclid’s Elements had defined space; it was based on 5 postulates, five things that were assumed to be true about geometry: for example, all right angles are equal to one another.
The fifth of Euclid’s five postulates was the parallel postulate. Euclid considered a straight line crossing two other straight lines. If the interior angles add to less than 180 degrees. In these circumstances, he said that the two straight lines will eventually meet. It was an unproven assertion and many mathematician up to the time of Gauss had tried to prove it. Gauss had been involved in a geodetic survey of the Kingdom of Hanover, linking up with previous Danish surveys (1818). This experience might have started him thinking about spherical geometry, curved two-dimensional surface such as the surface of a globe. Here the vertical lines of longitude all make angles of 90 degrees with the equator on the globe’s surface, yet by the time they reach the poles they have met. So the parallel postulate is incorrect on curved surfaces. Gauss realized that self-consistent non-Euclidean geometries could be constructed. He realized that the parallel postulate can never be proven, because the existence of non-Euclidean geometry shows this postulate is independent of Euclid’s other four postulates.
