83.
a^3: *
The first 4 spatial dimensions, represented in a 2D.
1 2 points can be connected to create a line segment.
2 2 parallel line segments can be connected to form a square.
3 2 parallel squares can be connected to form a cube.
4 2 parallel cubes
84.
a^n: *
In classical mechanics, space & time are different categories, refer to absolute space & time, a 4-dimensional space. The four dimensions of spacetime consist of events that are not absolutely defined spatially and temporally, but rather are known relative to the motion of an observer; 10 dimensions are used to describe string theory, 11 dimensions can describe supergravity and M-theory, and the state-space of quantum mechanics is an infinite-dimensional function space.
85.
groups: *
an algebraic structure consisting of a set of elements which when used with an operation (e.g. one of: +, -, * ,/) that combines any 2 elements to form a 3rd element, and which satisfies 4 conditions (group axioms):
closure (performance of an operation on members of the set always produces a member of the same set,
e.g. group or set of all real numbers, 5*4=20, 20 is a member of the set all real numbers);
associativity (the order in which the operations are performed does not matter as long as the sequence of the operands is not changed
e.g. 4*5*18= 18*5*4);
identity (an element of the which when combined with a binary operation (eg + or *) on that set, leaves other elements unchanged
e.g. for adding real numbers , 0 or multiplying real numbers the reciprocal);
invertibility (their exists an element that can 'undo' the effect of combination with another given element
e.g. negation will reverse addition).
86.
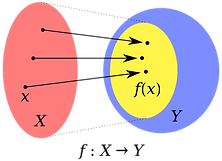
mathematical images: *
f is a function from domain X to codomain Y.
The yellow oval inside Y is the image of f.
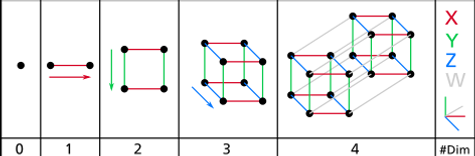
87.
differential equations: *
for example Newton's 2nd law of motion — the relationship between the displacement x and the time t of an object under the force F, is given by the differential equation which constrains the motion of a particle of constant mass m. In general, F is a function of the position x(t) of the particle at time t. The unknown function x(t) appears on both sides of the differential equation, and is indicated in the notation F(x(t)).

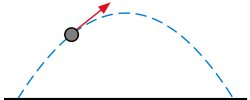
The trajectory of a projectile launched from a cannon follows a curve determined by an ordinary differential equation that is derived from Newton's second law.