54.
irrationals: *
Famous irrational numbers are the ratio of a circle's circumference to its diameter (pi), Euler's number e, the golden ratio & the square root of 2, all square roots of natural numbers, other than of perfect squares.
55.
“cut” (in Dedekind’s sense): *
a method of constructing the real numbers; a partition of the rational numbers into two non-empty sets A & B, such that all elements of A are less than all elements of B, and A contains no greatest element. B may or may not have a smallest element among the rationals; if it does then the cut corresponds to that rational smallest element, otherwise, the cut defines a unique irrational number which fills the "gap" between A and B. A contains every rational number less than the cut; B contains every rational number greater than or equal to the cut. An irrational cut is equated to an irrational number which is in neither set. Every real number, rational or not, is equated to one and only one cut of rationals.
56.
linear continuum: *
57.
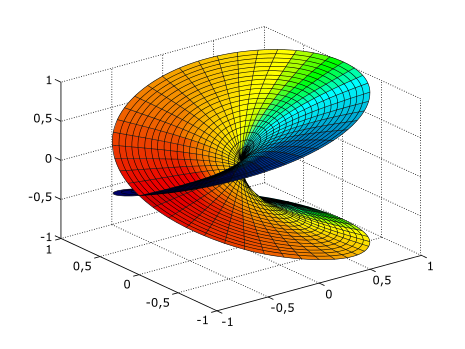
number surfaces: *
In complex analysis (mathematics) a Riemann surface, is a one-dimensional complex manifold, a deformed version of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different (e.g. they can look like a sphere or a torus or several sheets glued together).
Riemann surface for the function ƒ(z) = √z. The two horizontal axes
represent the real and imaginary parts of z, while the vertical axis
represents the real part of √z. For the imaginary part of √z, rotate the
plot 180° around the vertical axis.
