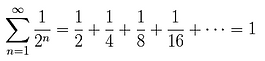49.
function: *
An example is the function that relates each real number x to its square x^2. The output of a function f corresponding to an input x is denoted by f(x) (read "f of x"). In this example, if the input is −3, then the output is 9, and we may write f(−3) = 9. Likewise, if the input is 3, then the output is also 9, and we may write f(3) = 9.
50.
complex numbers: *
today Imaginary & complex numbers are regarded just as "real" as real numbers, and are fundamental for many aspects describing the natural world. A complex number can be visually represented as a
pair of numbers (a, b) forming a vector on a diagram called an Argand diagram (a modified
Cartesian plane), representing the complex plane. "Re" is the real axis, "Im" is the imaginary
axis, and i satisfies i^2 = −1. The concept of the complex plane allows a geometric interpretation
of complex numbers.
Complex analysis (aka the theory of functions of a complex variable) investigates functions of complex numbers.
51.
Infinite series & Newton's binomial: *
In this example the infinite series is said to be convergent (on 1)
Newton’s binomial series is a binomial raised to the nth power, represented as (x + y)^n and it can be expanded by means of the binomial theorem.
The most basic example of the binomial theorem is the formula for the square of x + y: the square of the binomial (x + y) is equal to the sum of the squares of the two terms and twice the product of the terms, that is:
52.
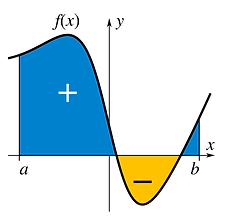
definite integral: *
Given a function f of a real variable x and an interval [a, b] of the real line, the definite integral
is defined informally as the signed area of the region in the xy-plane that is bounded by the graph
of f, the x-axis and the vertical lines x = a and x = b. The area above the x-axis adds to the total and
that below the x-axis subtracts from the total.
53.
aggregate as a new number: *
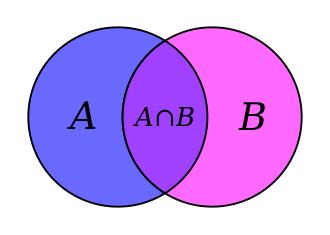
Venn diagram showing 3 sets, set A, set B and set union A&B