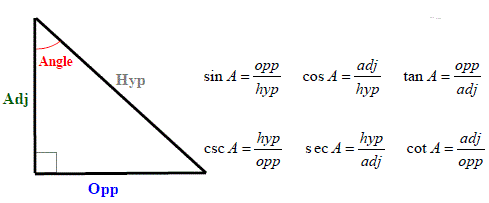
47.
Manifold of points: *
In general, any object that is nearly "flat" on small scales is a manifold, and so manifolds constitute a generalization of objects we could live on, in which we would encounter the round/flat Earth problem; concisely, any object that can be "charted" is a manifold. In topology, one describes a manifold using an atlas, which consists of individual charts that describe individual regions of the manifold. If the manifold is the surface of the Earth, then an atlas has its more common meaning. One-dimensional manifolds include lines & circles. Two-dimensional manifolds called surfaces include the plane, the sphere, and the torus all of which can all be formed without self-intersections in three dimensional real space.
ILLUSTRATION
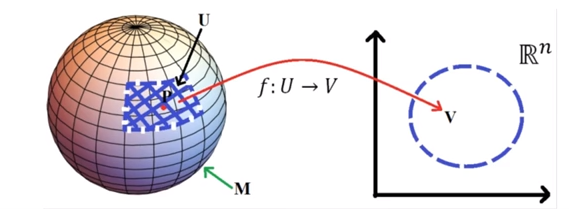
M is manifold M
R^n is a local space which is an n dimensional Euclidean space
P is a point in M;
there exists in M a set of points (a neighborhood) containing P, called U
M has a countable number of sets (not infinite)
we are able to map U to R^n with a function that takes the set U
into the set V contained in R^n space; the mapping function
is called a chart or coordinate system
V is the image of set U with a 1:1 mapping;
the image of point P (x^1…x^n) are the coordinates of P in the chart
a set of charts which define all possible sets is the atlas of M
48.
angular functions: *
illustration of the 6 trigonometric functions