36.
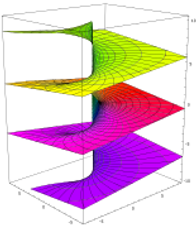
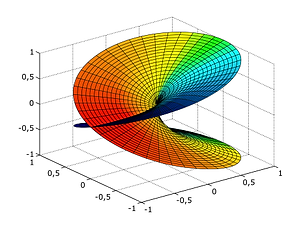
Riemann (and the symbolism of the 2 planes): *
locally near every point they look like patches of the
complex plane, but the global topology can be quite
different, they can look like a sphere or a torus or
several sheets glued together.
Riemann surface for the functions: f(z)= log z ƒ(z) = √z.
37.
Diophantus (influence of Indian, early Arabian): *
He clearly breaks from Greek thinking; developed his ideas without references to geometry; included symbols for unknowns (very un-Greek); first Greek mathematician who recognized fractions as numbers & allowed positive rational numbers for the coefficients & solutions, & accepted that a negative multiplied by negative resulted in a positive.
He does have some basic Greek foundations: he only gives single solutions to equations where there might be an indefinite number of solutions, & these solutions are never irrational or negative; although he uses symbols for unknowns, tends to use 1 or few of these, and also tends to describe an operation in words were an equation with symbols (symbolic logic) would have served as well.
38.
Renaissance mathematics (and Classicizing tendency): *
Greek texts were especially favored in the Renaissance. Late 16th century mathematics came under 2 influences: the Greeks (who provided geometry) & the Arabs (who provided algebra based on procedures for solutions or lists of rules). Vieta revolutionized the conventional way of thinking about constructing problems through the introduction of coordinate geometry; interested primarily in the properties of algebraic curves (especially of Diophantine equations); he was swimming against the Renaissance currents as he favored algebra over geometry.