28.
Apollonius: *
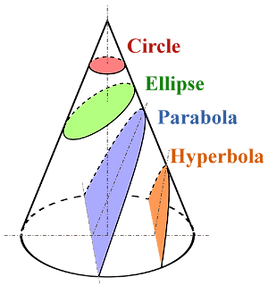
The conic sections, or two-dimensional figures formed by the intersection of a plane with a cone at different angles. The theory of these figures was developed extensively by the ancient Greek mathematicians, surviving especially in works such as those of Apollonius of Perga. The conic sections pervade modern mathematics.
29.
exhaustion method Archimedes: *
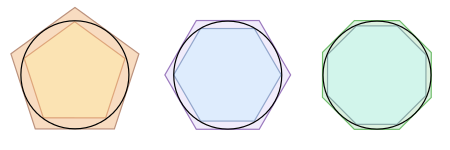
Archimedes used the method of exhaustion as a way to compute the area
inside a circle by filling the circle with a polygon of a greater area and greater
number of sides.
30.
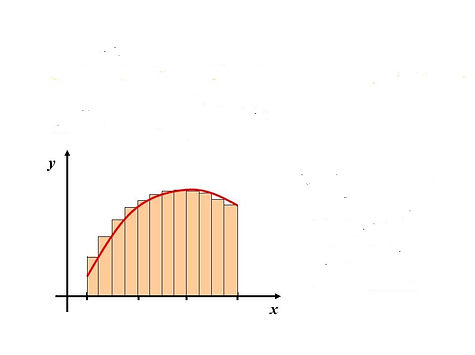
inscribed rectangles: *
R^n is the sum of all the inscribed
rectangles starting at the right endpoints.
31.
Riemann’s integral: *
The integral as the area of a region S
under a curve defined by the function (x)
32.
quadratures: *
In medieval Europe, quadrature meant the calculation of area by any method, usually the method indivisibles was used; using it Galileo found the area of a cycloid arch. Grégoire de Saint-Vincent investigated the area under a hyperbola & his student Alphonse Antonio de Sarasa, noted the relation of this area to logarithms. John Wallis algebrised this method (1656). The quadrature of the hyperbola by Saint-Vincent & de Sarasa provided a new function, the natural logarithm, of critical importance. With the invention of integral calculus came a universal method for area calculation.
33.
bounding function: *
A schematic illustration of a bounded
function (red) and an unbounded one (blue).
Intuitively, the graph of a bounded function
stays within a horizontal band, while the
graph of an unbounded function does not.
34.
cubic style (early Egyptians): *
illustration: mastaba of Faraoun at Saqqarah