xx.
Oresme:
He proved the divergence of the harmonic series (which is a divergent infinite series).
A divergent series is the opposite of a convergent series; if a series converges, the individual terms of the series must approach zero; any series in which the individual terms do not approach zero diverges (the infinite sequence of the partial sums of the series does not have a finite limit). However, convergence is a stronger condition. Not all series whose terms approach zero converge.
A counterexample is the harmonic series shown below-
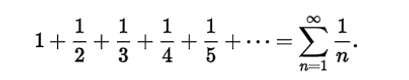
24.
Non Euclidean Goemetry:*
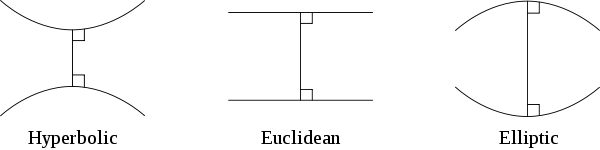
Three types of geometry are illustrated below:

Elliptical geometry started with the search to understand the movement of stars and planets in the apparently hemispherical sky. In addition to looking to the heavens, the ancients attempted to understand the shape of the Earth and to use this understanding to solve problems in navigation over long distances (and later for large-scale surveying). It has long been observed that the shortest distance between two points on Earth were great circle routes. Great circles are the “straight lines” of spherical geometry. This is a consequence of the properties of a sphere, in which the shortest distances on the surface are great circle routes. Such curves are said to be “intrinsically” straight. (Note, however, that intrinsically straight and shortest are not necessarily identical, as shown in the figure.). Three intersecting great circle arcs form a spherical triangle; while a spherical triangle must be distorted to fit on another sphere with a different radius, the difference is only one of scale. Spherical geometry does not define elliptic geometry, but is rather a subset of elliptic geometry. In differential geometry, spherical geometry is described as the geometry of a surface with constant positive curvature. see illustration

Riemannian geometry (aka elliptical geometry) originated with the vision of Bernhard Riemann in his 1854 inaugural lecture ("On the Hypotheses on which Geometry is Based"), a broad and abstract generalization of the differential geometry.
Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. The theory of plane & space curves & surfaces in the 3-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century &19th centuries.
Development of Riemann geometry resulted in a synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics. A geodesic (originally) was the shortest route between two points on the Earth's surface; it has been generalized to include measurements in much more general mathematical spaces, for example, in graph theory, one might consider a geodesic between two nodes of a graph. His work produced techniques that can be applied to the study of differentiable manifolds of higher dimensions. Riemannian’s geometry generalized to higher dimensions, in particular 4 dimensions with time integrated with space. This 4D Riemann geometry was heavily used by Einstein in developing his General Relativity.
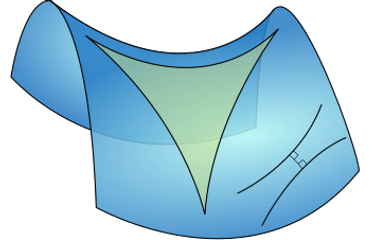
Below is a hyperbolic paraboloid (a saddle-shape plane) with an imposed triangle as well as two diverging ultraparallel lines (non-intersecting line having a point of minimum distance & diverging from both sides of that point)
Hyperbolic geometry was based on studies of Euclid’s 5th (“parallel”) postulate (see illustration below).
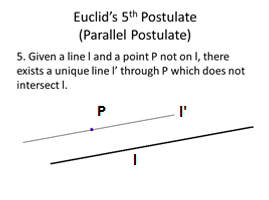
For any given line l and point P not on l, in the plane containing both line l and point P there are at least two distinct lines through P that do not intersect l. (see illustration)
For centuries mathematicians attempted either to prove the postulate as a theorem or modify it. In1829 Russian Nikolay Lobachevsky (1829) & Hungarian János Bolyai (1831) independently published a description of a geometry that, except for the parallel postulate, satisfied all of
Euclid’s postulates and common notions. It is this geometry that is called hyperbolic geometry.
Hyperbolic geometry is the geometry you get by assuming all the postulates of Euclid, except the fifth one, which is replaced by its negation.

Describing the 3 geometries.
Consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular to a third line:
• In Euclidean geometry the lines remain at a constant distance from each other (meaning that a line drawn perpendicular to one line at any point will intersect the other line and the length of the line segment joining the points of intersection remains constant) and are known as parallels.
• In hyperbolic geometry they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels.
• In elliptic geometry the lines "curve toward" each other and intersect.